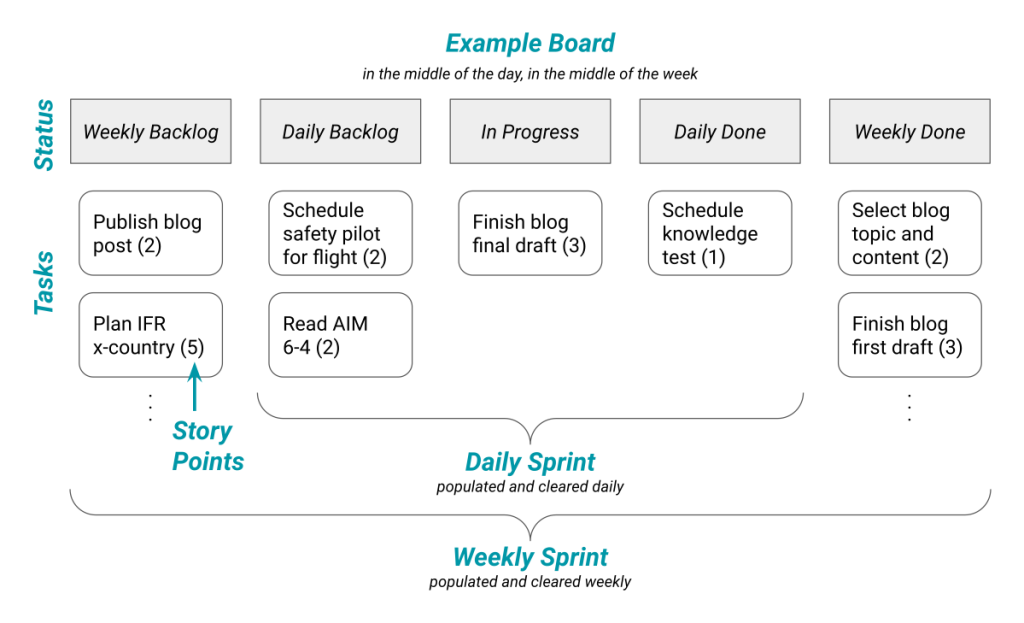
The boring way to convert knots to mph is to multiply knots by 1.15.1 But this skips over some awesome unit magic.
Specifically, we can use conversion factors to change between related units. Let’s look again at how to convert knots to mph.
Suppose you’re traveling at 
. Then,
![\[v\ \frac{\cancel{\text{nautical miles}}}{\text{hour}} * \frac{1.15\ \text{miles}}{1\ \cancel{\text{nautical miles}}} = v * 1.15\ \frac{\text{miles}}{\text{hour}}} = v * 1.15\ \text{mph}\]](https://cfijack.com/wp-content/ql-cache/quicklatex.com-9ff1370c9c805e275a9a0b753c85122f_l3.png "Rendered by QuickLaTeX.com")
Did You Just Cross Out the Units?
I did! This is called a conversion factor,2 and is based on the principle that anything multiplied by 1 equals itself. It is an easy way to convert between units, and allows us to solve a variety of aviation problems.
For instance, we know
and so
To convert knots to mph, we multiply our original speed by this conversion factor. We then cancel out common units on the top and bottom of the equation.3 So,
![\[v\ \frac{\cancel{\text{nautical miles}}}{\text{hour}} * \frac{1.15\ \text{miles}}{1\ \cancel{\text{nautical miles}}} = v * 1.15\ \frac{\text{miles}}{\text{hour}}}\]](https://cfijack.com/wp-content/ql-cache/quicklatex.com-e75f7c347a9653d85632802d1b009e49_l3.png "Rendered by QuickLaTeX.com")
Practical Uses
Complex Conversions
This approach is particularly handy for complex unit conversions. For instance, suppose your fuel burn is 10 gallons per hour, and you want to know how much weight you’ll lose after flying for 30 minutes.
To find the fuel consumed, convert 
to 
, then multiple by 30 minutes. This looks like,
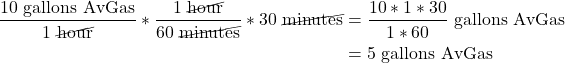
To find the weight equivalent, we know 
, so
![\[5\ \cancel{\text{gallons AvGas}} * \frac{6\ \text{lbs}}{1\ \cancel{\text{gallons AvGas}}} = 30\ \text{lbs}\]](https://cfijack.com/wp-content/ql-cache/quicklatex.com-ab9acdf67e2e43d93e635f4932b07d1c_l3.png "Rendered by QuickLaTeX.com")
If you’re feeling ambitious, you can do the whole conversion in one equation:
![\[\frac{10\ \cancel{\text{gallons AvGas}}}{1\ \cancel{\text{hour}}} * \frac{1\ \cancel{\text{hour}}}{60\ \cancel{\text{minutes}}} * 30\ \cancel{\text{minutes}} * \frac{6\ \text{lbs}}{1\ \cancel{\text{gallons AvGas}}} = 30\ \text{lbs}\]](https://cfijack.com/wp-content/ql-cache/quicklatex.com-0107f479bac50e93dfeda4ca876931dd_l3.png "Rendered by QuickLaTeX.com")
Plausibly Useful Idea: Canceling Terms After Factorization
A related idea is using factorization to simplify the math of equations like the one above.
To do this, we first factor out4 common terms in both the numerator and denominator. We can then cancel those common terms.
Using the example above,
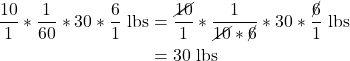
Unusual Unit Types
Conversion factors also make handling uncommon unit types easier. One unit we encounter in weight & balance is 
, the unit of a moment.
To find the center of gravity (
), we divide the total moment 
by the total weight 
. We can sanity check this logic by canceling units and confirming we end with 
.
![\[CG = \frac{M_{total}\ \text{\cancel{lb}-inches}}{w_{total}\ \cancel{\text{lb}}}=\frac{M_{total}}{w_{total}}\ \text{inches}\]](https://cfijack.com/wp-content/ql-cache/quicklatex.com-76e2bc87c9a5a0f89c5d8598f727cbdb_l3.png "Rendered by QuickLaTeX.com")
Knowledge Test Questions
Another powerful use for conversation factors is reasoning through knowledge test questions. For instance, if you encounter this problem,
If fuel consumption is 75 pounds per hour and groundspeed is 110 knots, how many gallons of fuel are required for an airplane to travel 380 NM?
Based on King School’s FAA Commercial Prep Questions
you can find a solution with conversation factors:((We can use the factorization method here as well:
![\[\frac{75\ \cancel{\text{lbs}}}{1\ \cancel{\text{hour}}} * \frac{1\ \cancel{\text{hour}}}{110\ \cancel{\text{nautical miles}}} * 380\ \cancel{\text{nautical miles}} * \frac{1\ \text{gallons AvGas}}{6\ \cancel{\text{lbs}}} = 43.18\ \text{gallons AvGas}\]](https://cfijack.com/wp-content/ql-cache/quicklatex.com-2202b0a6988b3e99d6021bc845101830_l3.png "Rendered by QuickLaTeX.com")
I find myself using this trick nearly every time I’m working with units — I hope you find it useful as well!
And of course, if you’re in the Bay Area and interested in learning to fly, shoot me a message and I’d be happy to meet you!
Best,
Jack
P.s. This post’s LaTeX functions were made possible by QuickLaTeX.
- This is actually more like 1.150779, but we’ll use the rounded version. ↩︎
- More precisely, you may hear this called dimensional analysis or the factor-label method. ↩︎
- We can cancel these out because $\frac{\text{miles}}{\text{miles}} = 1$. ↩︎
- Meaning break the number into smaller numbers that multiply back to the original number, such as $60 = 10 * 6 = 10*3*2$. ↩︎
